阅读说明

为了让每个算法模块能够有更多的的目录层级，本文直接将各模块单列出一个章节讲，这样的弊端是，知识点看起来比较乱，
一眼看不出他们对应的是什么算法内容。
所以本章节用于将各章节对应的算法知识点，进行目录分类。具体模块内容请跳转到相关章节看。

算法模块：

数组

电话号码

卡牌分组

种花问题

排序

冒泡排序

选择排序

快速排序

插入排序

最大间距 (冒泡排序实现)

数组中的第K个最大元素 (冒泡排序实现)

递归

复原ip地址

递归阶乘

斐波那契数

数据结构

二叉树

对称二叉树

验证二叉搜索树

基础算法篇

电话号码

概述

力扣原题 – 电话号码的字母组合
给定一个仅包含数字 2-9 的字符串，返回所有它能表示的字母组合。
给出数字到字母的映射如下（与电话按键相同）。注意 1 不对应任何字母。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
function calc(str) {
     let map = ['', 1, 'abc', 'def', 'ghi', 'jkl', 'mno', 'pqrs', 'tuv', 'wxyz']
     let num = str.split('')
     let code = []
     num.forEach(item => {
       if (map[item]) {
         code.push(map[item])
       }
     })
     let comb = (arr) => {
       // 临时变量用来保存前两个组合的结果
       let tmp = []
       // 最外层的循环是遍历第一个元素，里层的循环是遍历第二个元素
       for (let i = 0; i < arr[0].length; i++) {
         for (let j = 0; j < arr[1].length; j++) {
           tmp.push(`${arr[0][i]}${arr[1][j]}`)
         }
       }
       arr.splice(0, 2, tmp)
       if (arr.length > 1) {
         comb(arr)
       } else {
         return tmp
       }
       return arr[0]
     }
     return comb(code)
   }

   //calc('32')

现在对上面方法进行思路和要点解析

每次只让第一个和第二个元素两两组合

不管输入多少位数，都让前两位数字进行组合，组合的结果 再跟 第三位数字进行组合，逻辑一样，依次类推。 逻辑一样的部分，则突出了使用递归的需求。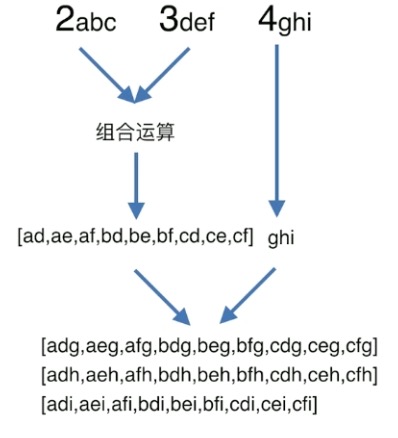

递归是重头戏

参考上面《两两组合》

return arr[0] 很需要

咋一看，觉得这一句不需要，以为有 if else，就不会走到 return arr[0]。这也是我误解的，其实下面的comb(arr)递归，执行完后，就会执行后面的return arr[0]。
以上也是我对于递归的误区。

1
2
3
4
5
6
7
if (arr.length > 1) {
       comb(arr)
   } else {
       return tmp
   }

return arr[0]

递归完了还会往下执行

参考上面 《return arr[0] 很需要》

解决方法优化

上面解决代码中，

1
2
3
4
5
6
if (arr.length > 1) {
         comb(arr)
       } else {
         //带有一定歧义
         return tmp
       }

可写成如下方式：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
function calc(str) {
   let map = ['', 1, 'abc', 'def', 'ghi', 'jkl', 'mno', 'pqrs', 'tuv', 'wxyz']
   let num = str.split('')
   let code = []
   num.forEach(item => {
     if (map[item]) {
       code.push(map[item])
     }
   })
   let comb = (arr) => {
     // 临时变量用来保存前两个组合的结果
     let tmp = []
     // 最外层的循环是遍历第一个元素，里层的循环是遍历第二个元素
     for (let i = 0; i < arr[0].length; i++) {
       for (let j = 0; j < arr[1].length; j++) {
         tmp.push(`${arr[0][i]}${arr[1][j]}`)
       }
     }
     arr.splice(0, 2, tmp)
     if (arr.length > 1) {
       return comb(arr)
     }else{
       return arr[0]
     }
   }
   return comb(code)
 }

再一次优化

上面的代码看起来有点晕，下面将两两组合的逻辑提出来，让代码更清晰，本次优化的逻辑与上面是一样的：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
function combile(a1,b1){
    let arr=[];
    a1.forEach(ai=>{
        b1.forEach(bi=>{
            arr.push(`${ai}${bi}`);
        })
    })
    return arr;
}
function calc1(str){
   let map = ['', 1, 'abc', 'def', 'ghi', 'jkl', 'mno', 'pqrs', 'tuv', 'wxyz'];
   const allStr = str.split('').map(num=>map[Number(num)]);
   const cur = (strarr)=>{
     //第一次strarr[0]是一个字符串， 以后strarr[0]经过splice后，都是数组
    const one = typeof strarr[0] === 'string' ? strarr[0].split('') : strarr[0];
    const two = strarr[1].split('');
    const newItem0 = combile(one, two);
    strarr.splice(0,2,newItem0);
       if(strarr.length<2){
           return strarr[0];
       }
     return cur(strarr)
   }
  return cur(allStr);
}

考察算法要点

给定一个数组，如何让内部元素两两组和，返回一个全组合结果；
其核心思想是，不管数组有多少元素，每次只让第一个元素和第二个元素两两组和；
递归以上行为，经过递归后，最终数组只有一个元素。这个元素就是组合结果。
所以核心是第一个和第二个两两组和；
技术实施是递归；
利用的原则是数组两两组和到最后必然只有一个元素；

卡牌分组

概述

给定一副牌，每张牌上都写着一个整数。
此时，你需要选定一个数字 X，使我们可以将整副牌按下述规则分成 1 组或更多组：
每组都有 X 张牌。
组内所有的牌上都写着相同的整数。
仅当你可选的 X >= 2 时返回 true。
力扣原题 – 卡牌分组

用白话解释原题：给定一副牌，这副牌可以是1张或1万张，将这副牌分成一组或多组，每组牌的数字都相同，每组牌的个数不少于2.

解法一： 数组前后两两比较

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
function calc(arr) {
      // 将卡牌按值排序保证相同的卡牌是挨着的
      let str = arr.sort((a, b) => a - b).join('')
      // 分组(单张或者多张)  \1 在正则中表示连续一样的匹配
      let group = str.match(/(\d)\1+|\d/g)
      // 求两个数的最大公约数
      let gcd = (a, b) => {    
        if(b === 0)  return a;   
        return gcd(b, a % b)
       }
      // 思想：只要所有的分组具有最大公约数(大于1)就满足条件
      // 对所有的分组进行最大公约数验证，相邻两个分组的最大公约数，再与后面的公约数进行验证，以此类推，有一个最大公约数为1就退出
      while (group.length > 1) {
        let a = group.shift().length
        let b = group.shift().length
        let v = gcd(a, b)
        if (v === 1) {
          return false
        } else {
          // 将前两个分组的最大公约数推进数组与下一个分组再次验证是否有最大公约数
          group.unshift('0'.repeat(v))
        }
      }
      // 考虑边界['11']即只有一个分组的时候
      return group.length ? group[0].length > 1 : false
    }

最大公约数

代码实现

下面是最大公约数的求法，可以不必理解，知道这样用就行

1
2
3
4
let gcd = (a, b) => {    
    if(b === 0)  return a;   
    return gcd(b, a % b)
}

最大公约数除了1值外，其他值都合法

数组前后两两比较

1
2
3
4
5
while (group.length > 1) {
        let a = group.shift().length
        let b = group.shift().length
      ...
      }

找出元素出现次数的方法(推荐)–match正则

1
2
// 分组(单张或者多张)  \1 在正则中表示连续一样的匹配
 let group = str.match(/(\d)\1+|\d/g)

找出元素出现次数的方法–object key方式

参考下面的《最小相同数与所有相同数比较的 实现方式》

1
2
3
4
5
6
7
8
const hash = deck.reduce((pre, num) => {    //统计出每种数字的数目
  if(!pre[num]) {
    pre[num] = 1
  }else{
    pre[num]++
  }
  return pre
}, {})

while 实现 递归效果

见上面的代码。

解法一优化：用递归代替while写法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
function calc(arr) {
     let str = arr.sort((a, b) => a - b).join('')
     let group = str.match(/(\d)\1+|\d/g)
     let gcd = (a, b) => {    
       if(b === 0)  return a;   
       return gcd(b, a % b)
      }
      const cur = (arr)=>{
        if(arr.length<2){
          return arr[0].length > 1;
        }
        const one = arr.shift().length;
        const two = arr.shift().length;
        let v = gcd(one, two);
        if (v === 1) {
         return false
       } else {
         arr.unshift('0'.repeat(v));
        return cur(arr);
       }
      }
     return cur(group);
   }

解法二：最小相同数与所有相同数比较

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
var hasGroupsSizeX = function(deck) {
  let getResult = (a, b) => {    //定义一个寻找公约数的方法
    if(b === 0)  return a;   
    return getResult(b, a % b)
  }
  const hash = deck.reduce((pre, num) => {    //统计出每种数字的数目
    if(!pre[num]) {
      pre[num] = 1
    }else{
      pre[num]++
    }
    return pre
  }, {})
  const numCount = Object.values(hash)     //将hash中的每项数值存入数组，便于后续遍历
  const min = numCount.sort((a, b) => a-b)[0];         //利用数组排序快速获取最小值
  if (min < 2) return false; //根据题意，如果最分组最小数量小于2，直接返回false
  return !numCount.some((item,index) => {
    if(index > 0) return getResult(item, min) === 1
  })
}

两种方案的利弊

尽管两种方法都能实现，但是解法一比解法二节省了一次遍历，当数据量大时，这种性能上的差别就会比较大，所以推荐第一种方案。

种花问题

概述

假设你有一个很长的花坛，一部分地块种植了花，另一部分却没有。可是，花卉不能种植在相邻的地块上，它们会争夺水源，两者都会死去。
给定一个花坛（表示为一个数组包含0和1，其中0表示没种植花，1表示种植了花），和一个数 n 。能否在不打破种植规则的情况下种入 n 朵花，算出n的最大值。
力扣原题 – 种花问题

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
function calc(arr){
    // 计数器
    let max = 0
    for (let i = 0; i < arr.length - 1; i++) {
      //只有arr[i] === 0时，说明可以种花，因此只需考虑arr[i] === 0的逻辑，其他情况不用考虑
      if (arr[i] === 0) {
        //当 arr[i] === 0 时都符合条件，唯有边界值 i===0 与 i === arr.length-2 时需要特殊考虑
        if (i === 0 && arr[1] === 0) {
          max++
          //跳转，这里i++，加上for循环自动也++，所以i实际加了2
          i++
        } else if (i === arr.length-2 && arr[arr.length-1] === 0) {
          max++
        }else if (arr[i - 1] === 0 && arr[i + 1] === 0) {
          max++
           //跳转，这里i++，加上for循环自动也++，所以i实际加了2
          i++
        }
      }
    }
    return max
  }

  calc([1, 0, 0, 0, 1, 0, 0])// 2
  calc([1, 0, 0, 0, 1])//1
  calc([0,0,1, 0, 0, 0, 1])//2

要点分析

1
[1,0,0,0,0,0,0,0,1]

其实就是在数组中找000的模型，有000就可以变成010，达到要求。
另外一个要考虑的是边界问题，比如，[0,0,1]，这不符合 000，但依然可以在最左侧加1；
这种问题其实就是在数组中找 000 这种模型，就涉及到用数学建模的思想来解决。

核心一： 000的数学建模

以后遇到类似的找这种000的形式的东西，就考虑用数学建模。

核心二： 遍历

种花问题，主要运用遍历来解决，使用了很多遍历技巧，比如跳级忽略遍历，以及i+1等的处理，
i+1的遍历技巧本质上就是多个遍历元素的技巧；
因为一般遍历元素只有一个arr[i]（姑且称这种遍历为单元遍历）,多个遍历元素是指遍历体中同时存在 arr[i] arr[i+n] （多元遍历）。

单元遍历 与 多元遍历

参考《核心二： 遍历》

遍历体用 i++ 跳级忽略遍历

例如下面的，index位置 1 2 3 符合 000；
2 3 4 也符合 000；

1
[1,0,0,0,0,1]

但实际上当遍历了index 123后，下一次只要求遍历index 345；
如何做到呢，可通过在for循环内，i++ :

1
2
3
4
for (let i = 0, len = arr.length - 1; i < len; i++) {
   //跳转，这里i++，加上for循环自动也++，所以i实际加了2
   i++
}

边界问题

参考《要点分析》

arr[i+1]与arr[i-1]的遍历技巧

arr[i-1] 与 arr[i+1] 与 i<arr.length-1 的妙用

因为for循环体内用了arr[i+1]，那么在for的title上能遍历的最大值是 arr.length - 2，也就是i < arr.length - 1；
这个是一个很实用的用法，我们在写for循环时，如果for循环体内有这样的情况，就应该考虑好for的title上最大的i < arr.length值也应响应配合增加或减少。并且这个最大的arr.length值到底多少与函数体内最大的arr[i+1]有关，而与arr[i-1]无关。，当然，如果用到arr[i-1]时，就要考虑边界值的问题，也就是当i为0时的情况。

1
2
3
4
5
6
for (let i = 0; i < arr.length - 1; i++) {
       ...
         } else if (arr[i - 1] === 0 && arr[i + 1] === 0) {
       ...
       
     }

arr[i-1]时考虑边界值，arr[i-1]时考虑i值最大值

参考《arr[i-1] 与 arr[i+1] 与 i<arr.length-1 的妙用》

遍历的经典练习题

种花问题基于遍历实现，用到了比较多的遍历技巧，可称为经典遍历的运用练习题。

冒泡排序

概述

冒泡排序大白话解释就是，将数组内的最大值，从左到右或右带左地排序，这个过程好像数组内的最大值好像冒泡一样，从水底上浮的过程。
冒泡排序是每次比较左右两个值，每次进行比较交换位置。

如下图，要实现如下的一个渐进的排序过程：


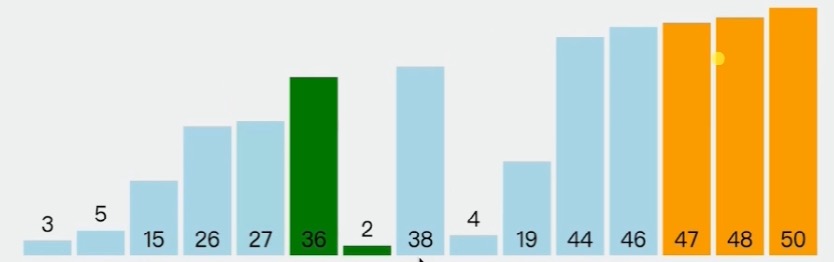
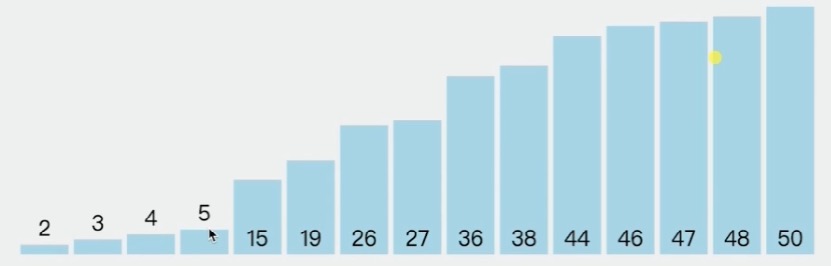
将最值移到边缘的技巧

1
2
3
4
5
6
7
for (let j = 0; j < arr.length-1; j++) {
            if (arr[j] > arr[j + 1]) {
            let c = arr[j];
            arr[j] = arr[j + 1]
            arr[j + 1] = c;
            }
        }

排序是最值移动的多次重复

既然有一种算法可以将最值移动至边缘，那么这种算法就构成了排序的可能，我们可以将最值移动称之为排序的最小组成。
就好比，复杂的现象 无非都是 将简单的现象重复多遍的结果。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
function calc(arr) {
    // 冒泡排序
    for (let i = arr.length - 1; i > 0; i--) {
        for (let j = 0; j < i; j++) {
            if (arr[j] > arr[j + 1]) {
            let c = arr[j];
            arr[j] = arr[j + 1]
            arr[j + 1] = c;
            }
        }
    }
    return arr;
}

calc([1, 9, 5, 3, 4,0,2,999,6]) //[0, 1, 2, 3, 4, 5, 6, 9, 999]

原理

通过最值移动，将最值移至边缘，那么下次遍历的时候，只需排除这个最值，将剩余的元素重复最值的移动。
现在最值移动的算法我们已经知道了，要做的是，每次最值移动时不包含边缘的最值。

处理i+1 遍历的技巧

参考 《将最值移到边缘的技巧》

选择排序

概述 以及 选择、冒泡区别

如下图，要实现如下的一个渐进的排序过程：

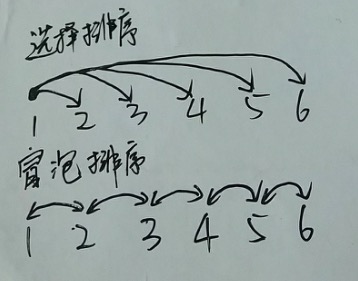
选定第1个位置放置最小值

1
2
3
4
5
6
7
8
var i = 0 //第1个位置
 for (let j = i + 1; j < len; j++) {
          if (arr[j] < arr[i]) {
            let c = arr[i]
            arr[i] = arr[j]
            arr[j] = c
          }
        }

选定第2个位置放置剩余数组的最小值

1
2
3
4
5
6
7
8
var i = 1 //第2个位置
 for (let j = i + 1; j < len; j++) {
          if (arr[j] < arr[i]) {
            let c = arr[i]
            arr[i] = arr[j]
            arr[j] = c
          }
        }

实现

将上面选定位置最值算法重复多遍，就达到排序的效果。

1
2
3
4
5
6
7
8
9
10
11
12
13
function calc(arr) {
      // 选择排序
      for (let i = 0, len = arr.length; i < len; i++) {
        for (let j = i + 1; j < len; j++) {
          if (arr[j] < arr[i]) {
            let c = arr[i]
            arr[i] = arr[j]
            arr[j] = c
          }
        }
      }
      return arr
    }

最大间距

概述

力扣原题 – 最大间距
给定一个无序的数组，找出数组在排序之后，相邻元素之间最大的差值。
如果数组元素个数小于 2，则返回 0。

推荐方法

介绍

这种题一般通过排序完成，并且在排序的过程中，获取最大值，以下通过 冒泡排序的方式来做，主要利用冒泡的时候，其他已经逐步排序好最大值了，利用这逐步排序好的最大值，逐步求出间距：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
function getDistance(a, b, max) {
     const num = a - b;
     if (max < num) {
       max = Math.abs(num);
     }
     return max;
   }
   function calc(arr) {
     let max=0;
     for (let i = arr.length - 1, tmp; i > 0; i--) {
       for (let j = 0; j < i; j++) {
         if (arr[j] > arr[j + 1]) {
           let c = arr[j];
           arr[j] = arr[j + 1];
           arr[j + 1] = c;
         }
       }
       if (i < (arr.length - 1)) {
         max = getDistance(arr[i + 1], arr[i], max);
         if (i === 1) {
           max = getDistance(arr[1], arr[0], max);
         }
       }
     }
     return max;
   }

边界处理

当i === (arr.length - 2)与i=1时需要处理不同逻辑。

借助冒泡或选择排序实现

如上代码，因为冒泡或选择排序是，最左或最右端值已经排序好，排序好的就可以计算差值。所以可利用这一特性，找出最大间距。

不推荐方法

不推荐理由，利用sort进行了一次遍历，然后又用遍历求最大间距，用了两次遍历，相比上面的推荐方法的一次遍历，这种方法性能不好。

遍历是核心

最大间距的解决主要借助遍历实现。

数组中的第K个最大元素

力扣原题 – 数组中的第K个最大元素
在未排序的数组中找到第 k 个最大的元素。请注意，你需要找的是数组排序后的第 k 个最大的元素，而不是第 k 个不同的元素。
示例 1:
输入: [3,2,1,5,6,4] 和 k = 2
输出: 5
示例 2:

输入: [3,2,3,1,2,4,5,5,6] 和 k = 4
输出: 4
说明:

先说不推荐方法

不推荐方法

这种方法非常容易理解，但是却有浪费之嫌，因为根本不需要对整个数组先排序再查找，因为一旦找到第k个值，就可以停止程序了。

1
2
3
export default (arr, k) => {
  return arr.sort((a, b) => b - a)[k - 1]
}

推荐方法

利用冒泡排序来做：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
export default (arr, k) => {
  let len = arr.length - 1
  for (let i = len, tmp; i > len - k; i--) {
    for (let j = 0; j < i; j++) {
      if (arr[j] > arr[j + 1]) {
        tmp = arr[j]
        arr[j] = arr[j + 1]
        arr[j + 1] = tmp
      }
    }
  }
  // arr[len+1-k]
  return arr[len - (k - 1)]
}

借助冒泡或选择排序实现

如上代码，因为冒泡或选择排序是，最左或最右端值已经排序好，排序到第k个时，马上停止遍历，有助于性能。

快速排序(最好的排序方式)

要点分析

快速排序，以数组中间一个元素为基准，小于的放在左边，大于的放在右边，然后递归，排序完成。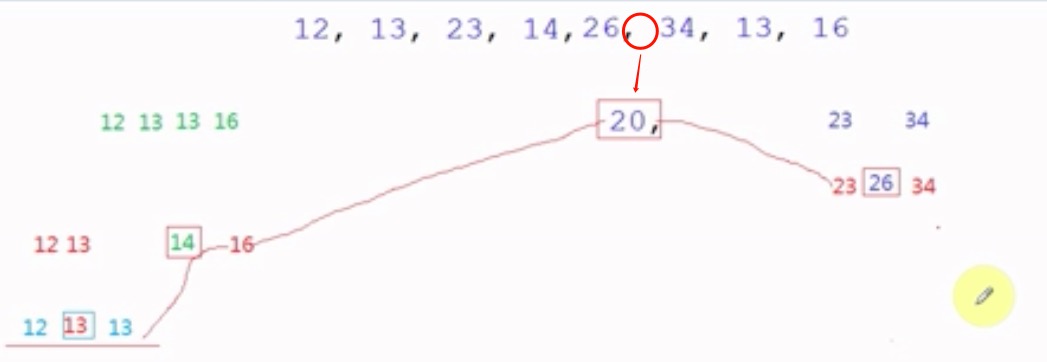

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
function quickSort(ary){
       if(ary.length<=1){
           return ary;
       }
       var pointIndex = Math.floor(ary.length/2);
       //从ary中删除pointIndex，并且通过[0]取出pointValue值
       var pointValue = ary.splice(pointIndex, 1)[0];
       var left = [];
       var right = [];
       for (var i=0; i<ary.length; i++){
           var cur = ary[i];
           cur < pointValue ? left.push(cur) : right.push(cur);
       }
       return quickSort(left).concat([pointValue],quickSort(right));
   }

中间元素，左右两边分组

快速排序是选一个数组中间元素值为准，左右分两组，这种操作类似易经大衍筮法占卜的手法。
不过快速排序不是一定要数组中间值，任意一个元素为准都可以，只是推荐使用中间元素。

推荐使用中间元素,但也可使用其他元素

这里有一个以其他元素为准的快速排序写法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
function quickSort(arr) {
    if (arr.length <= 1) {
        return arr;
    }
    let leftArr = [];
    let rightArr = [];
    let q = arr[0];
    for (let i = 1, l = arr.length; i < l; i++) {
        if (arr[i] > q) {
            rightArr.push(arr[i]);
        } else {
            leftArr.push(arr[i]);
        }
    } 
    return [].concat(quickSort(leftArr), [q], quickSort(rightArr));
}

递归的经典运用

递归是快速排序的核心，如果无法理解，暂且就记住这种场景解法，用多了，自然就有了这种逻辑思维了。

递归最后呈现的由最后的边界值决定

比如上面的代码:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
function quickSort(ary){
       if(ary.length<=1){
           return ary;//这是边界值
       }
       var pointIndex = Math.floor(ary.length/2);
       //从ary中删除pointIndex，并且通过[0]取出pointValue值
       var pointValue = ary.splice(pointIndex, 1)[0];
       var left = [];
       var right = [];
       for (var i=0; i<ary.length; i++){
           var cur = ary[i];
           cur < pointValue ? left.push(cur) : right.push(cur);
       }
       return quickSort(left).concat([pointValue],quickSort(right));//return 表达式
   }

无论quickSort(left)递归了多少次，quickSort(left)的值，肯定是 ary ，
同理，quickSort(right))的值，肯定是 ary。

递归结果是边界值与return表达式作用的结果

因此，无论怎么样，quickSort(ary)执行的结果，必将形式如下：

1
quickSort(left).concat([pointValue],quickSort(right))

经过上面的分析，quickSort(left)等效 ary，
上面等效

1
[1].concat([1],[1])

这说明了，递归最后呈现的由最后的边界值决定，且返回的结果 就是边界值与return表达式作用的结果。

插入排序

通常方案

概述

将原来数组打散重新将所有元素一个个放置，新建一个数组，用于接收放置的元素。
元素在新数组中，按照大小顺序插入放置。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
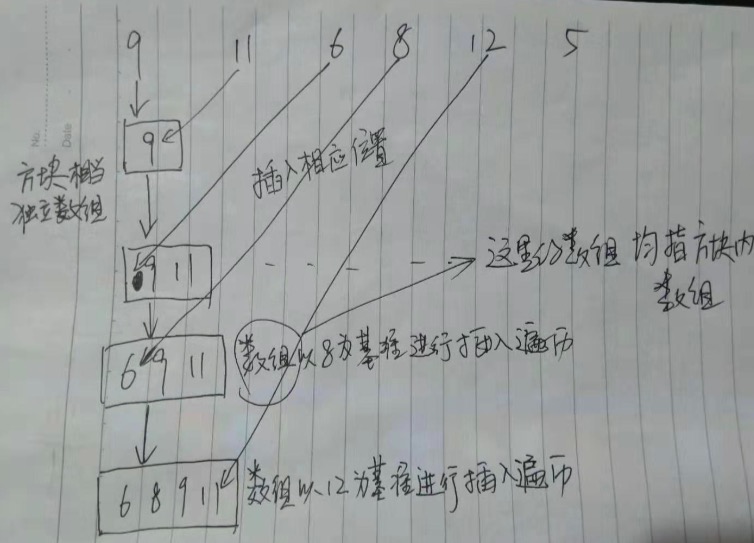
21
 function insertSort(ary){
    var newAry=[];
    newAry.push(ary[0]);
    for(var i=1; i<ary.length; i++){
        var cur =ary[i];
        for(var j = newAry.length - 1; j>=0;j--){
            //其实这里就考虑两种情况，将最大值放入右侧，或者找不到最大值，就说明这个是最小值，放入左侧，
            if(cur>newAry[j]){
                newAry.splice(j+1,0,cur);//最大值放到右侧
                break;
            }else{
              //j===0，数组表示遍历完了，说明此时数组的全部元素都大于cur
                if(j===0){
                  newAry.unshift(cur);//最小值放入左侧
                  break;//这个break可以不用，写出来，只是方便理解，告诉你，如果改变了newAry，那么将结束遍历
                }
            }
        }
    }
    return newAry;
}

提高

可不用了解

下面的提高做法，是网上比较流行的插入排序算法，有精力可以了解下

不新建数组直接排序的实现

这种方法与方案一不同的是，方案二没有单独创建新数组来存放排序元素，而是直接基于原数组进行改造，相对来说理解起来要难一点。
其实找到窍门后，理解起来就好了，理解插入排序，只需要理解内层遍历如何排序，就理解了整个插入排序的思想，后面有讲到。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
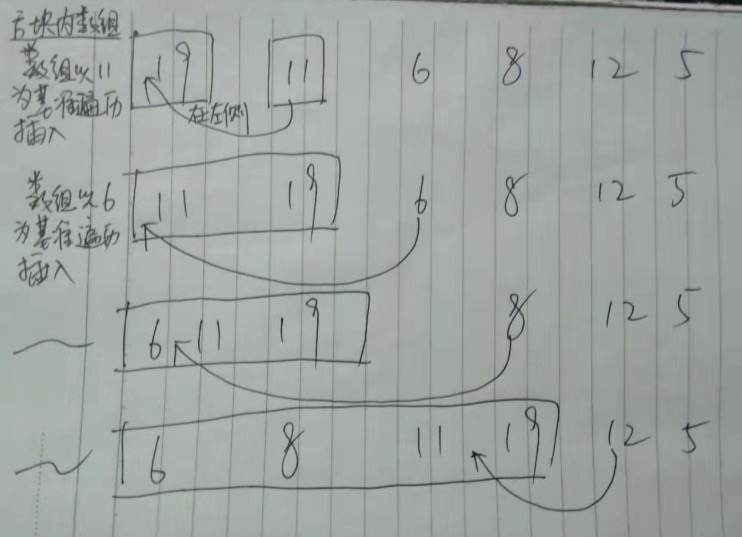
21
 function insertSort(ary){
    var key,j;
    for(var i=1;i<ary.length;i++){
            key=ary[i];
            for(var j=i-1;j>-1;j--){
                if(ary[j]>key){
                  如果ary[j]大于key，那么将ary[j]往右挪一步
                    ary[j+1]=ary[j];
                    if(j===0){
                        //能走到j===0说明ary[j]都大于key，原来的j 数组已经整体往右挪一步，此时ary[0]值就是key；
                        ary[0]=key;
                    }
                }else{
                    如果ary[j]小于key，那么将key置于其右侧
                    ary[j+1]=key;
                    break;
                }
            }
        }
        return ary;
}

外层遍历提供元素，内层遍历进行排序

内层排序技巧

外层遍历每次给内层遍历输入一个元素；
内层遍历 接收这个元素后，如何排序；
接收一个元素势必增加长度；
所以通过j+1，通过比较，数组整体平移整个数组：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
key=ary[i];
            for(var j=i-1;j>-1;j--){
                if(ary[j]>key){
                  如果ary[j]大于key，那么将ary[j]往右挪一步
                    ary[j+1]=ary[j];
                    if(j===0){
                        //能走到j===0说明ary[j]都大于key，原来的j 数组已经整体往右挪一步，此时ary[0]值就是key；
                        ary[0]=key;
                    }
                }else{
                    如果ary[j]小于key，那么将key置于其右侧
                    ary[j+1]=key;
                    break;
                }
            }

遍历的经典应用

此方案是经典的

用while来改写方案二

此写法其思想跟方案二是一样的。
while的好处是代码十分简洁，但是此代码极具误导性，单凭此，就可以认定这种写法是不推荐的。
这里有一个理解误区，a[0] 可以进入 while体内，等出来的时候j就变成了 -1 ，ary[-1+1]就是a[0]。

1
2
3
4
5
6
7
8
9
10
11
12
13
function insertSort1(ary){
    var key,j;
    for(var i=1;i<ary.length;i++){
            key=ary[i];
            j=i-1;
            while(j>-1&&ary[j]>key){
                ary[j+1]=ary[j];
                j--;
            }
            ary[j+1]=key;
        }
        return ary;
}

复原ip地址

概述

给定一个只包含数字的字符串，复原它并返回所有可能的 IP 地址格式。
示例:
输入: “25525511135”
输出: [“255.255.11.135”, “255.255.111.35”]
力扣原题 – 复原IP地址

用白话解释原题：给出一串字符，写出它能组成的所有的ip.

解决方法

代码如下，个人觉得代码不容易理解，请先看下面当代码分析

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
function calc(str) {
      // 保存所有符合条件的IP地址
      let r = []
      // 分四步递归处理ip分段
      let search = (cur, sub) => {
        // 非法输入过滤 ip地址最多不超过12个字符长
        if (sub.length > 12) {
          return
        }
        // 边界条件
        if (cur.length === 4 && cur.join('') === str) {
          r.push(cur.join('.'))
        } else {
          // 正常的处理过程 
          // Math.min(3, sub.length) i必须小于等于3
          for (let i = 0, tmp; i < Math.min(3, sub.length); i++) {
            tmp = sub.substr(0, i + 1)
            if (tmp - 256 < 0) {
              const newCur = cur.concat([tmp]);
              const newSub = sub.substr(i + 1);
              //当 newCur的数组元素超过4时，就不是ip地址了；
              //当newCur有三个元素，准备补充第四个元素时，如果第四个元素当字符长度大于3位，就没有必要再继续下去
              if(newCur.length > 4 || (newCur.length === 3 && newSub.length>3)){
                continue
              }
              search(newCur, newSub)
            }
          }
        }
      }
      search([], str)
      return r
    }

代码分析

如下图，25525511135 这样一个字符串，要组成一个ip时；
ip由四个不大于256的数字排列组成；
第一个数字可以是 2 25 255；
当第一个数字为2时 剩下的代码为 5525511135；
此时它的第二个数字可以是 5 55 552(大于256，不符合规则)；
当第二个数字为5时，剩下的代码为 525511135；
此时它第三个数字可以是 5 52 525；
当第三个数字为5时， 剩下代码为25511136 不符合规则；
依次类推–递归。
如果你还是对分析或则上面代码不太理解，请拿出你对纸和笔，将上面代码在纸上遍历几次，就明白了。

递归设计中 必不可少的 边界条件

要写一个递归，必须要写终止递归条件，也就是边界条件。上面代码的边界条件就是：

1
2
3
if (cur.length === 4 && cur.join('') === str) {
         r.push(cur.join('.'))
       }

对称二叉树

力扣原题–对称二叉树

创建对称二叉树

二叉树模型图

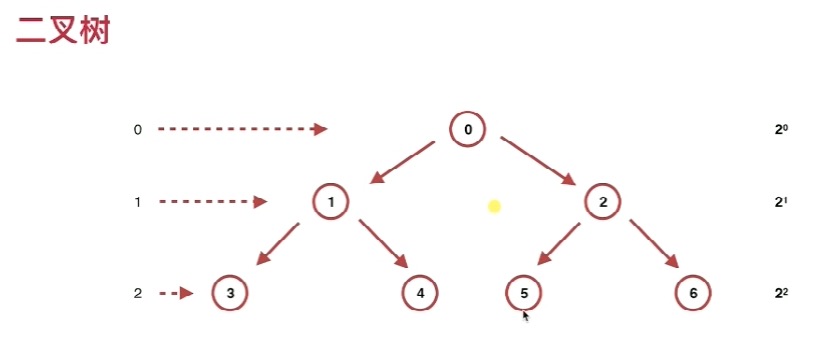
代码

以下是创建二叉树代码，后面会针对代码疑问进行解答

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
 // 二叉树的节点
class Node {
  constructor(val) {
    this.val = val
    this.left = this.right = undefined
  }
}

class Tree {
  constructor(data) {
    // 临时存储所有节点，方便寻找父子节点
    let nodeList = []
    // 顶节点
    let root
    for (let i = 0, len = data.length; i < len; i++) {
      let node = new Node(data[i])
      nodeList.push(node)
      if (i > 0) {
        // 计算当前节点属于那一层
        let n = Math.floor(Math.sqrt(i + 1))
        // 记录当前层的起始nodelist的index
        let q = Math.pow(2, n) - 1
        // 记录上一层的起始nodelist的index
        let p = Math.pow(2, n - 1) - 1
        // 找到当前节点的父节nodelist的index
        let parent = nodeList[p + Math.floor((i - q) / 2)]
        // 将当前节点和上一层的父节点做关联
        if (parent.left) {
          parent.right = node
        } else {
          parent.left = node
        }
      }
    }
    //只有第一个元素是起始节点，
    root = nodeList.shift()
    //其他元素完成使命，可以去掉
    nodeList.length = 0
    return root
  }
  //验证二叉树是否是对称
  static isSymmetry(root) {
    if (!root) {
      return true
    }
    let walk = (left, right) => {
      if (!left && !right) {
        return true
      }
      if ((left && !right) || (!left && right) || (left.val !== right.val)) {
        return false
      }
      return walk(left.left, right.right) && walk(left.right, right.left)
    }
    return walk(root.left, root.right)
  }
}

new Tree([1, 2, 2, 3, 4, 4, 3])
//返回：
const tree = {
  "val": 1,
  "right": {
    "val": 2,
    "right": {
      "val": 3
    },
    "left": {
      "val": 4
    }
  },
  "left": {
    "val": 2,
    "right": {
      "val": 4
    },
    "left": {
      "val": 3
    }
  }
}

当前节点属于那一层

如果理解不了，请记住，这是业内得出的公式，无需太较真理解，记住这个定理公式就行。

1
2
// 计算当前节点属于那一层
 let n = Math.floor(Math.sqrt(i + 1))

记录当前层的起始nodelist的index

由上面的二叉树模型图看出，每一层的元素的起始点起始就是前面所有层元素个数之和，
而这个和的值正好是2的n次幂，所以每一层对应到nodelist数组的index就是如下公式：

1
2
3
4
// 记录当前层的起始 nodelist的index
  let q = Math.pow(2, n) - 1
  // 记录上一层的起始 nodelist的index
  let p = Math.pow(2, n - 1) - 1

每一层有多少个元素

参考上面《记录当前层的起始nodelist的index》

找到当前节点的父节nodelist的index

1
2
// 找到当前节点的父节点
        let parent = nodeList[p + Math.floor((i - q) / 2)]

有几个知识点要了解：
当前层的起始点 Math.pow(2, n) - 1 ，例如第二层，起始点是3；
那么这个3就是上面代码中的nodelist的index，
第一层，起始点是0；那么这个0就是nodelist的index；
所以上面代码中 进行for遍历时，i就是nodelist的下标，q或p也是nodelist的下标。
由于每两个子节点对应一个父节点，所以需要除以2

数组每个元素都生成一个node节点

1
2
3
 for (let i = 0, len = data.length; i < len; i++) {
      let node = new Node(data[i])
...

利用node节点Object浅拷贝特性

利用这一浅拷贝特点，让第一个数组元素成为所有数组其他元素形成的节点的共同父节点。

1
2
3
4
5
6
7
let parent = nodeList[p + Math.floor((i - q) / 2)]
       // 将当前节点和上一层的父节点做关联
       if (parent.left) {
         parent.right = node
       } else {
         parent.left = node
       }

验证二叉树是否是对称

实现

代码见上面《创建二叉树》

递归

主要运用了递归原理验证二叉树是否对称。

验证二叉搜索树

力扣原题–验证二叉搜索树

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
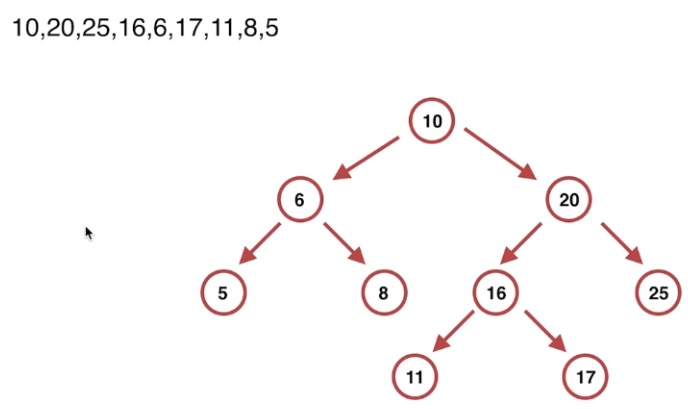
43
class Node {
  constructor (val) {
    this.val = val
    this.left = this.right = undefined
  }
}

class Tree {
  constructor (data) {
    let root = new Node(data.shift())
    // 遍历所有的数据，逐渐插入到当前这棵搜索树中去
    data.forEach(item => {
      this.insert(root, item)
    })
    return root
  }
  insert (node, data) {
    if (node.val > data) {
      if (node.left === undefined) {
        node.left = new Node(data)
      } else {
        this.insert(node.left, data)
      }
    } else {
      if (node.right === undefined) {
        node.right = new Node(data)
      } else {
        this.insert(node.right, data)
      }
    }
  }
  static walk (root) {
    if (!root.left && !root.right) {
      return true
    } else if ((root.left && root.val < root.left.val) || (root.right && root.val > root.right.val)) {
      return false
    } else {
      return Tree.walk(root.left) && Tree.walk(root.right)
    }
  }
}

 new Tree([2, 1, 3,6,8,9])

小左大右

本搜索二叉树按照左大右小排列。

递归

上面代码中，无论生成二叉树与验证二叉树都使用了二叉树，注意递归中 边界值处理技巧。

递归

递归的结构

每个递归由一个递归体以及一个边界值组成。且必须有一个边界值。

阶乘

1
2
3
4
5
6
7
function foctorial(n){
  if(n === 1 || n === 0){
    return 1;
  }
  return n * foctorial(n-1)
}
foctorial(5)//120

边界值(又称基线条件)

边界值与基线条件是一个道理，即一个停止点。
如下，递归中，很多最终都是通过边界值来计算，且终止递归。

1
2
//我们只需写出边界（1）的实现就行。
foctorial(5) = 5*4*3*2*(1)；

边界值：

1
2
3
if(n === 1 || n === 0){
   return 1;
 }

斐波那契数

概念

斐波那契数列 是一个由 0, 1, 1, 2, 3, 5, 8, 13, 21 等组成等序列。数2由1加1得到，数3由2加1得到…。
斐波那契数列有个定义：

  • 位置0的数是0；
  • 1和2的数是1；
  • n(n>2)的数是n-1、 n-2 之和。

    实现一（常规实现）

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    function fn(n){
         if(n<1) return 0;
         if(n<=2) return 1;
         let prepreStartval = 0;
         let preStartval = 1;
         //前一个的前一个位置的值
         let prepre=prepreStartval;
         //前一个位置的值
         let pre=preStartval;
         //本位置的值
         let item= '';
         for(let i=2;i<=n;i++){
             //本位置的值 = 前一个位置值 + 前一个的前一个位置值
             item=pre+prepre;
             //新的前一个的前一个的值 变成上个位置的前一个位置的值
             prepre=pre;
             //新的前一个的值 变成上一个位置的值
             pre=item;
         }
         return item;
     }

实现二 （递归实现）

1
2
3
4
5
function fn(n){
    if(n<1) return 0;
    if(n<=2) return 1;
    return fn(n-1) + fn(n-2);
}

配合

1
2
3
4
5
6
7
8
 function calculate(n, fn){
    var arr=[];
    for(var j=0; j<n; j++){ 
        arr[j]=fn(j) 
    } 
    return arr; 
}
calculate(8, fn)  // [0, 1, 1, 2, 3, 5, 8, 13]

实现三 （记忆化优化）

1
2
3
4
5
6
7
8
9
10
11
function calcFactory(){
    const memo = [0, 1];
    const fn=(n)=>{
        //memo[n]===0  0是非，但本例中是一个值；
        if(memo[n] || memo[n]===0) return memo[n];
        return memo[n] = fn(n-1) + fn(n-2);
    }
    return fn;
}
var calc = calcFactory()；
calc(8) //13;

边界值 与 最小化分析

很多递归问题或其他算法问题，他们几乎都是由最小值或边界值重复或计算而来，在解决问题时，可以将问题使用边界值最小化分析

递归记忆化技巧

参考《斐波那契数 – 实现三 （记忆优化）》

递归与while

有时候递归能实现的，通过while也能实现，while具有一些递归的质能。
参考《卡牌分组 — while 实现 递归效果》

递归经典应用示例

快速排序

参考《快速排序》

电话号码

参考《电话号码》

卡牌分组

参考《卡牌分组》

复原ip地址

参考《复原ip地址》

遍历

遍历类型

多元遍历

上面的 种花问题，冒泡排序， 选择排序，都是多元遍历的运用；

多层遍历

冒泡排序，选择排序 是多层遍历的运用；

跳级(忽略)遍历

参考 《种花问题 — 遍历体用 i++ 跳级忽略遍历》

多层遍历 内层遍历j+1

内外两层遍历，内层遍历通过j+1,腾出多一个位置来接收一个元素，进行排序的技巧，参考
《插入排序 — 方案二 (推荐)》

经典应用示例

插入排序 （非常经典）

是非常经典的排序方式，尤其是方案二。
插入排序与冒泡排序形成了两种思路的遍历思想；
插入由内部遍历排序，冒泡由外部遍历排序。

种花问题

这里是遍历的经典运用，参考《种花问题》

冒泡排序

参考《冒泡排序》

选择排序

参考《选择排序》

最大间距

参考 《最大间距》

数组中的第K个最大元素

参考 《数组中的第K个最大元素》

常用算法场景

数组前后两两比较

概述

参考：《电话号码》中的源码

1
2
3
4
5
6
7
8
9
10
11
const cur = (strarr)=>{
    //第一次strarr[0]是一个字符串， 以后strarr[0]经过splice后，都是数组
   const one = typeof strarr[0] === 'string' ? strarr[0].split('') : strarr[0];
   const two = strarr[1].split('');
   const newItem0 = combile(one, two);
   strarr.splice(0,2,newItem0);
      if(strarr.length<2){
          return strarr[0];
      }
    return cur(strarr)
  }

更多参考 《卡牌分组》

每次只比较数组的第一和第二项

1
2
3
const one = typeof strarr[0] === 'string' ? strarr[0].split('') : strarr[0];
const two = strarr[1].split('');
const newItem0 = combile(one, two);

删除第一和第二项，将比较结果重新置为第一项

如上代码，每次比较完第一和第二项后，删除他们，并将比较结果置为第一项

1
strarr.splice(0,2,newItem0);

递归是核心

见代码

边界值：strarr.length<2

两两比较到最后，数组只剩下一个元素，此时递归停止，所以边界值：strarr.length<2。

找出元素出现次数

找出元素出现次数的方法(推荐)–match正则

详细参考 《卡牌分组》

1
2
// 分组(单张或者多张)  \1 在正则中表示连续一样的匹配
 let group = str.match(/(\d)\1+|\d/g)

找出元素出现次数的方法–object key方式

详细参考 《卡牌分组》

1
2
3
4
5
6
7
8
const hash = deck.reduce((pre, num) => {    //统计出每种数字的数目
  if(!pre[num]) {
    pre[num] = 1
  }else{
    pre[num]++
  }
  return pre
}, {})

时间／空间复杂度

概述

简言之，
时间复杂度是对运行次数的描述，因为运行次数的多少决定了花多少时间。
空间复杂度是对运行内存的描述，在排序时定义了多少变量，就会消耗多少内存。
一般关注好时间复杂度即可。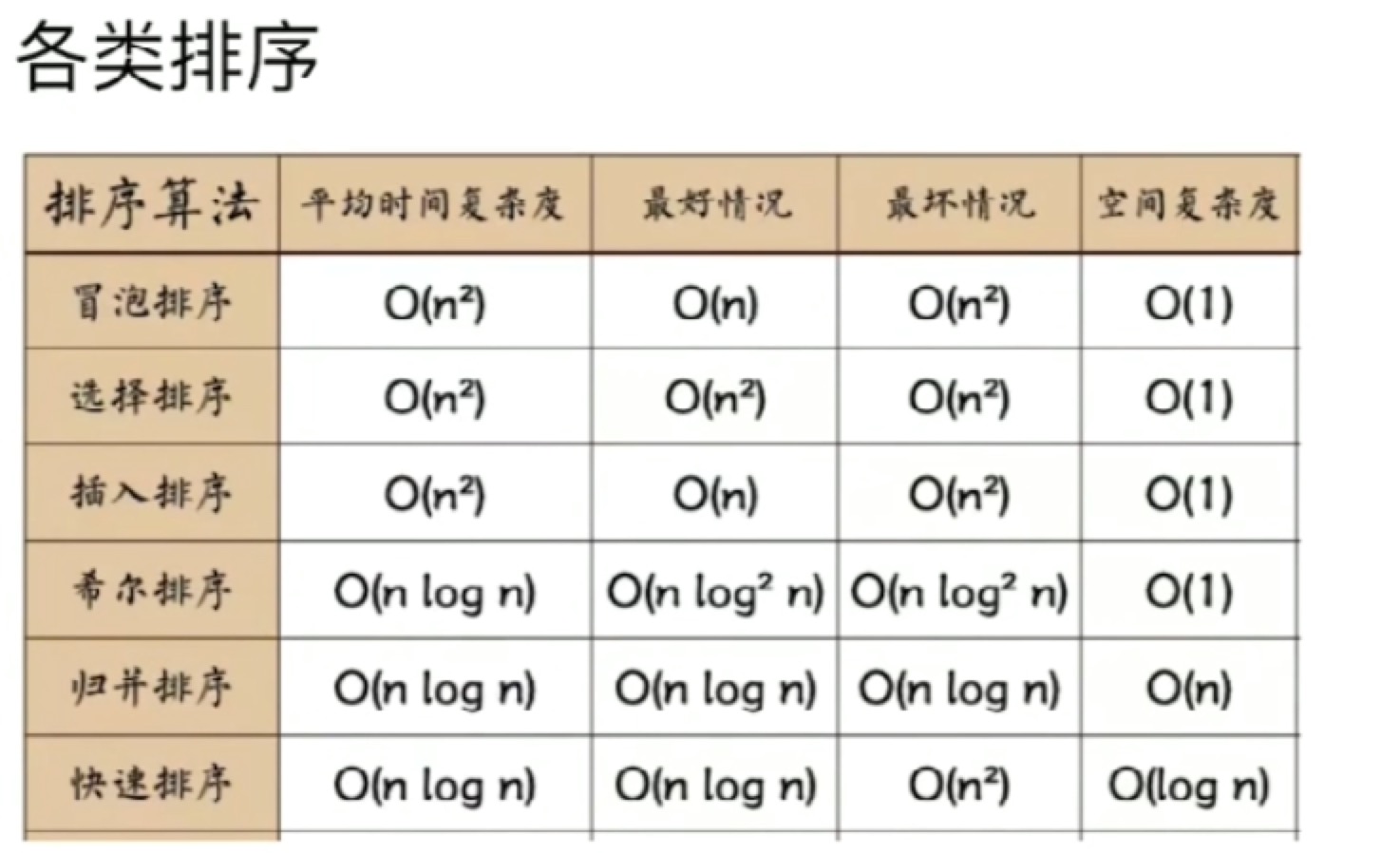

时间复杂度

1
2
3
4
//时间复杂度为 O(9)
for (let j = 0; j < 9; j++) {
     console.log(j)
  }
1
2
3
4
5
6
//时间复杂度为 O(9*9)
  for (let i = 9; i > 0; i--) {
        for (let j = 0; j < 9; j++) {
             console.log(j)
            }
        }

参考

JavaScript版 数据结构与算法
珠峰教育 –js排序
学习JavaScript数据结构与算法（第3版）